Final answer:
The Taylor series expansion for the functions sin(x), cos(x), and e^x, and their respective radii of convergence.
Step-by-step explanation:
The Taylor series expansion of a function is a way to approximate the function by using a polynomial.
(i) For the function sin(x), the Taylor series expansion is:
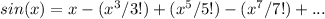 which means the series converges for all values of x.
which means the series converges for all values of x.
(ii) For the function cos(x), the Taylor series expansion is:
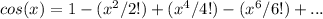 which means the series converges for all values of x.
which means the series converges for all values of x.
(iii) For the function e^x, the Taylor series expansion is:
 nite, which means the series converges for all values of x.
nite, which means the series converges for all values of x.