Question

Verify divergence theorem for the vector function F=(x2−z2)i^+2xyj^​+(y2+z)k^ taken over the region bounded by the cylinder x2+z2=9 and y=2,y=4

Answer 1

1. The divergence theorem verifies the flux of the vector field F through a closed surface is equal to the triple integral of the divergence of F over the region it encloses.

2. If f is an injection and gₖ is an injection, then gₖ₊₁ is an injection due to the composition of injective functions preserving injectivity.

Step-by-step explanation:

For the first part, applying the divergence theorem involves calculating the flux of the vector field F through the closed surface bounded by the cylinder
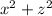`x^2 + z^2` = 9 and the planes y = 2 and y = 4. By evaluating the surface integral of the vector field over this closed surface and computing the triple integral of the divergence of F over the region it encloses, the equality is verified. The divergence theorem essentially relates the flux through a closed surface to the behavior of the vector field within the enclosed region, providing a convenient way to compute flux.

Regarding the second part, if f is an injection, meaning each element in the domain maps to a distinct element in the codomain, and gₖ is an injection, then their composition gₖ₊₁ remains injective. This is due to the nature of injective functions where different inputs result in different outputs, and composing two injective functions follows the same principle, preserving the property of injectivity for the resulting function gₖ₊₁.

The process of verifying the divergence theorem involves calculating surface and volume integrals to confirm the equality while the second part draws on the properties of injective functions, showing how the composition of injective functions maintains injectivity in the resultant function gₖ₊₁.