Question

Find the distance between the point P(4,-3) and Q(-3,5)

Answer 1

The distance between the points P(4,-3) and Q(-3,5) is approximately sqrt(113) units.

Step-by-step explanation:

To find the distance between two points in a Cartesian plane, we can use the distance formula. The formula is:
`d = \sqrt((x2 - x1)^2 + (y2 - y1)^2)`

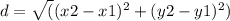
Using the given points, P(4,-3) and Q(-3,5), we can substitute the values into the formula:

`d = \sqrt((-3 - 4)^2 + (5 - (-3))^2)\\d = \sqrt((-7)^2 + (8)^2)\\d = \sqrt(49 + 64)\\d =\sqrt(113)`

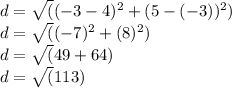
So, the distance between the points P(4,-3) and Q(-3,5) is approximately
`\sqrt(113)` units.

Answer 2

d ≈ 10.63 units

Step-by-step explanation:

calculate the distance, d, using the distance formula

d =
`\sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2 }`

let (x₁, y₁ ) = P (4, - 3 ) and (x₂, y₂ ) = Q (- 3, 5 )

substitute these values into the formula for d

d =
`√((- 3-4)^2+(5-(-3))^2)`

=
`√((-7)^2+(5+3)^2)`

=
`√(49+8^2)`

=
`√(49+64)`

=
`√(113)`

≈ 10.63 units ( to 2 decimal places )