Question

P = 100 - 20 cos (8πt/3) That's (8 pi t /3) where t is the time (in seconds). What is the period of the model? Discuss what the period represents in the context of this model.

Answer 1

The period of the model is
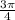`(3\pi)/(4)` seconds. The period represents the time needed for the function to complete one cycle.

Explanation:

Cosine is a trigonometric function and trigonometric functions are characterized by having a periodical behavior. The period is the time needed for the function to cover an angle of
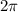`2\pi` radians. By this approach we find that:

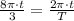`(8\pi\cdot t)/(3) = (2\pi\cdot t)/(T)` (1)

Where:

`t` - Time, measured in seconds.

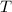`T` - Period, measured in seconds.

Then, we solve (1) for
`T`:

`(8)/(3) = (2\pi)/(T)`

`T = (6\pi)/(8)\,s`

`T = (3\pi)/(4)\,s`

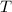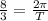
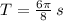
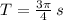
The period of the model is
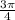`(3\pi)/(4)` seconds. The period represents the time needed for the function to complete one cycle.