Final answer:
To prove that the function
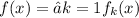 n use the Monotone Convergence Theorem (MCT). The Monotone Convergence Theorem states that if we have a sequence of nonnegative measurable functions {f_n} and
n use the Monotone Convergence Theorem (MCT). The Monotone Convergence Theorem states that if we have a sequence of nonnegative measurable functions {f_n} and
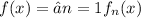 able.
able.
Step-by-step explanation:
To prove that the function
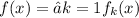 can use the Monotone Convergence Theorem (MCT).
can use the Monotone Convergence Theorem (MCT).
The Monotone Convergence Theorem states that if we have a sequence of nonnegative measurable functions {fn} and
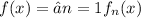 able.
able.
The proof involves showing that for any positive integer m, the set x is measurable. This can be done by showing that x is measurable for each n, and then taking the union over all n.