Question

Find the x-intercept and and y-intercept algebraically

y = log2 (x + 1) - 3

need work

Answer 1

x intercept is 7 y intercept is -3

Explanation:

Write equation out and have y=0

`log_(2)(x - 1) - 3 = 0`

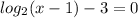
Add 3 to both sides

`log_(2)(x - 1) = 3`

Using the log to exponet rule

`(log_(b)(x) = y ) \: equal \: b {}^(y) = x`

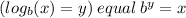
Where b and x are real numbers and b cannot equal 1.

Reorder the equation as a exponet

`log_(2)((x + 1) = 3`

`{2}^(3) = x + 1`

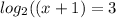
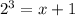
Simplify

`8 = x + 1`

Subtract 1 from both sides

`x = 7`

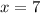
So the x intercept is 7

To find y intercept plug 0 in as x

`log_(2)(0 + 1) - 3 = y`

`log_(2)(1) - 3 = y`

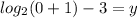
Add 3 to both sides

`log_(2)(1) = y + 3`

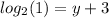
Rewrite in exponet form

`{2}^(y + 3) = 1`

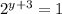
Using the zero exponet property, anything to the zero power equal 1 so we must find a value that equal out to zero using the exponet so we'll set up the equation

`y + 3 = 0`

Subtract 3 from both sides and we get

`y = - 3`

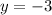
So the x intercept is 7 and the y intercept is -3