Answer:
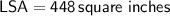

Explanation:
There are two types of areas in the triangular prism.
They are Lateral and Total surface area.
Let's calculate Lateral and Total Surface Area of Triangular Prism
Lateral Surface Area (LSA):
The lateral surface area of a triangular prism is the sum of the area of the three rectangular faces. We can calculate it using two formulas:
1. Formula 1:
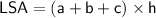
where:
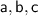 are the sides of the triangular base
are the sides of the triangular base
 is the height of the prism (which is also the length in this case)
is the height of the prism (which is also the length in this case)
2. Formula 2:
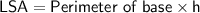
where:
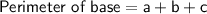
Using formula 1:
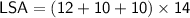
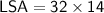
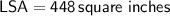
Using formula 2:
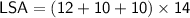
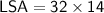
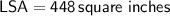
Therefore, the lateral surface area of the triangular prism is 448 square inches.
Total Surface Area (TSA):
The total surface area of a triangular prism is the sum of the lateral surface area and the area of the two triangular bases.
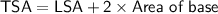
Area of base:
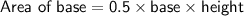
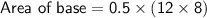
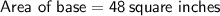
Total Surface Area:

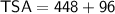

Therefore, the total surface area of the triangular prism is 544 square inches.