Question

Consider AABC - AXYZ.

What is the value of tan(A)?
What is the value of tan(X)?
What is true about the two tangent ratios?

Answer 1

The tangent ratios (tan(A)) and (tan(X)) are defined as the ratio of the opposite side to the adjacent side in their respective right-angled triangles. These ratios remain consistent across similar triangles.

The tangent ratio in a right-angled triangle is defined as the ratio of the length of the side opposite the angle ((A) or (X)) to the length of the adjacent side. Mathematically,
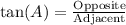`\(\tan(A) = \frac{\text{Opposite}}{\text{Adjacent}}\)` and
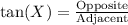`\(\tan(X) = \frac{\text{Opposite}}{\text{Adjacent}}\)`. These ratios represent the tangent of angle (A) and angle (X) in their respective triangles.

The values of (tan(A)) and (tan(X)) can be determined by knowing the lengths of the sides in the specific triangles. However, it's important to note that the tangent ratio is the same for both angles in a similar right-angled triangle, as it solely depends on the ratio of the opposite side to the adjacent side.