Question

The inspection division of the Lee County Weights and Measures Department is interested in estimating the actual amount of soft drink that is placed in 2-liter bottles at the local bottling plant of a large nationally known soft-drink company. A random sample of 64 bottles obtained from this bottling plant indicated a sample average and standard deviation of 2.99 and .06 liters repectively. Set up a 98% confidence interval estimate of the true average amount of soft drink in each bottle.

Answer 1

The 98% confidence interval estimate of the true average amount of soft drink in each bottle is between 2.97 liters and 3.01 liters.

Explanation:

We have the standard deviation for the sample, so we use the t-distribution to solve this question.

The first step to solve this problem is finding how many degrees of freedom, we have. This is the sample size subtracted by 1. So

df = 64 - 1 = 63

98% confidence interval

Now, we have to find a value of T, which is found looking at the t table, with 63 degrees of freedom(y-axis) and a confidence level of
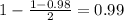`1 - (1 - 0.98)/(2) = 0.99`. So we have T = 2.387

The margin of error is:

`M = T(s)/(√(n)) = 2.387(0.06)/(√(64)) = 0.02`

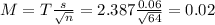
In which s is the standard deviation of the sample and n is the size of the sample.

The lower end of the interval is the sample mean subtracted by M. So it is 2.99 - 0.02 = 2.97 liters

The upper end of the interval is the sample mean added to M. So it is 2.99 + 0.02 = 3.01 liters

The 98% confidence interval estimate of the true average amount of soft drink in each bottle is between 2.97 liters and 3.01 liters.