Question

Logan is a land surveyor. He wants to determine d, the distance across a lake that cannot be directly measured. He draws this diagram to help him.

A right triangle with side length 7 kilometers, d, and hypotenuse of 9 kilometers.

What is the approximate distance across the lake, to the nearest tenth of a kilometer?
5.7 km
6.3 km
11.4 km
16.0 km

Answer 1

A

Explanation:

Answer 2

The first option (5.7km)

Explanation:

Since we have a right angle triangle and we know two of its sides we can easily find out the thirds side (the value of d) by using the Pathagoras Theorem. In our case 7 and d are our legs and the hypotenuse is equal to 9, so...

(Based on the Pathagoras Theorem)

`c^(2) = a^(2) + b^(2)`

`9^(2) = 7^(2) + d^(2)`

`d^(2) = 9^(2) - 7^(2) \\d^(2) = 81 - 49\\d^(2) = 32\\d = √(32)\\`

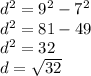
d ≈ 5.7km

There for aproximate distance across the lake is equal to 5.7km