Answer:
The first option (5.7km)
Explanation:
Since we have a right angle triangle and we know two of its sides we can easily find out the thirds side (the value of d) by using the Pathagoras Theorem. In our case 7 and d are our legs and the hypotenuse is equal to 9, so...
(Based on the Pathagoras Theorem)
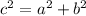
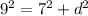
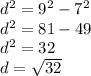
d ≈ 5.7km
There for aproximate distance across the lake is equal to 5.7km