Question

1. Show work. The electrostatic potential of a certain charge distribution with a total charge Q at a distance z from the distribution is given by V(z) = k Q, where b is a constant. Which of the given expressions best describes the electric field ? [hint, apply E= -VV(z)].​

Answer 1

For the given electrostatic potential V(z) = kQ, the electric field along the z-axis is
`\(E_z = 0\).`

The electric field (E) is related to the electrostatic potential (V) by the negative gradient of the potential. Mathematically, this relationship is expressed as
`\(E = -\\abla V\).`

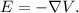
In one dimension, for a spherically symmetric charge distribution, the relationship between E and V is given by
`\(E = -(dV)/(dr)\)`, where r is the radial distance.

Given the electrostatic potential V(z) = kQ, where k is a constant, and Q is the total charge, we can find the electric field along the z-axis (
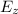`\(E_z\)`) as follows:

`\[E_z = -(dV)/(dz)\]`

`\[E_z = -(d)/(dz)(kQ)\]`

Since k and Q are constants, the derivative with respect to z is zero, and we have:

`\[E_z = 0\]`

Therefore, the expression that best describes the electric field in this case is
`\(E_z = 0\).`

The probable question may be:

The electrostatic potential of a certain charge distribution with a total charge Q at a distance z from the distribution is given by V(z) = k Q, where b is a constant. Which expression best describes the electric field? [hint, apply E= -VV(z)].​