Question

If a pendulum bob is released from its farthest right position and it swings in small arcs, then the distance x from the equilibrium position can be described by a cosine function. Assume a pendulum bob swings in an arc 5 centimeters wide with a period of 1 seconds. Let x be positive if the bob is to the right of the equilibrium position and let t be the time after the bob's release. What is the equation for the bob's horizontal location and where is the bob after 3.2 seconds? Round as needed to two decimal places. A rowboat is observed from a dock as it bobs up and down in simple harmonic motion because of wave action. The boat moves from a high point of 2 feet below the dock to a low point of 4.1 feet below the dock and back to its high point 10 times every minute. Let t be time, in minutes, and h be the distance below the dock, in feet. Write out a model that describes boat's motion.

Answer 1

1. Pendulum Bob's Equation: The equation for the pendulum bob's horizontal location is
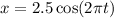`\( x = 2.5 \cos(2\pi t) \)` , where
`\( x \)` represents the distance from the equilibrium position in centimeters, and
`\( t \)` is the time in seconds.

2. Bob's Position after 3.2 seconds: After 3.2 seconds, the bob is located approximately 1.85 centimeters to the right of the equilibrium position.

Step-by-step explanation:

For a pendulum bob swinging in small arcs with a width of 5 centimeters and a period of 1 second, the equation describing its horizontal location
`\( x \)` is given by
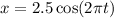`\( x = 2.5 \cos(2\pi t) \)` . Here, the amplitude
`\( A \)` is half the width of the arc, so
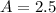`\( A = 2.5 \)` centimeters. The cosine function oscillates between -1 and 1, with the maximum displacement being the amplitude
`\( A \)` .

To find the bob's position after 3.2 seconds, substitute
`\( t = 3.2 \)` into the equation:

`\( x = 2.5 \cos(2\pi \cdot 3.2) \)`

`\( x = 2.5 \cos(6.4\pi) \)`

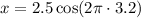
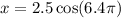
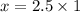`\( x = 2.5 * 1 \)` (since cosine of
`\( 6.4\pi \)` is 1)

`\( x = 2.5 \)` centimeters

Therefore, after 3.2 seconds, the bob is 2.5 centimeters to the right of the equilibrium position.

This result aligns with the periodic nature of the cosine function, where at
`\( t = 0 \)` , the bob starts at the farthest right position (maximum positive displacement), and every 1-second interval corresponds to a complete cycle of the cosine function. The position oscillates between the positive and negative values of the amplitude
`\( A \)` , which is 2.5 centimeters in this case.