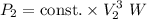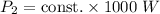Solution :
Given :
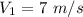
Operation time,
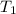 = 3000 hours per year
= 3000 hours per year
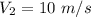
Operation time,
 = 2000 hours per year
= 2000 hours per year
The density, ρ =
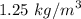
The wind blows steadily. So, the K.E. =
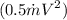

The power generation is the time rate of the kinetic energy which can be calculated as follows:
Power =
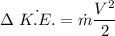
Regarding that
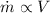 . Then,
. Then,
Power
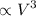 → Power = constant x
→ Power = constant x
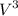
Since,
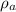 is constant for both the sites and the area is the same as same winf turbine is used.
is constant for both the sites and the area is the same as same winf turbine is used.
For the first site,
Power,
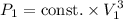
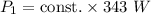
For the second site,
Power,