Question

Membership in the Cape Fear Health Club has been recorded for the past nine years. Management wants to determine the trend of membership in order to project future space needs. This estimate would help the club determine whether a future expansion will be needed. Given the following time series data, develop a regression equation relating memberships to years. Based on your regression equation, what is your forecast for 2020 memberships? Memberships are in hundreds.

Year > 2011 2012 2013 2014 2015 2016 2017 2018 2019
#'s > 11 13 15 17 16 18 20 19 23
a. 22.b. 24.6.c. 23.3.d. 11.e. 25.9.

Answer 1

c). 23.3

Step-by-step explanation:

Period Demand X Y XY
`$X^2$`

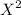
1 11 1 11 11 1

2 13 2 13 26 4

3 15 3 15 45 9

4 17 4 17 68 16

5 16 5 16 80 25

6 18 6 18 108 36

7 20 7 20 140 49

8 19 8 19 152 64

9 23 9 23 207 81

∑ 45 152 837 285

Intercept
`$(B_0) = \Sigma Y * \Sigma X^2 - \Sigma X * (\Sigma XY)/((N* \Sigma X^2 - \Sigma X^2)) $`

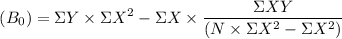
Intercept
`$= (152* 285)-(45 * 837)/((9 * 285)-45^2)$`

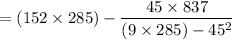
= 10.47

Slope
`$(B_1)= ((N* \Sigma XY) - (\Sigma X * \Sigma Y)-(N * \SIgma X^2 - \Sigma X^2)$`

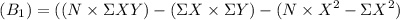
Slope
`$=((9*837)-((45 * 152))/((9 * 285)-45^2) $`

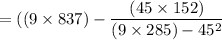
= 1.28

Therefore, the equation is

Y = intercept + slope(X)

`$Y=10.47 + (1.25 * X)$`

For
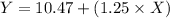
`$X=10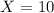$` forecast
`$= 10.47 + (1.28 * 10)$`

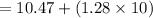
= 23.27 or 23.3