Question

A new medical test has been designed to detect the presence of the mysterious Brainlesserian disease. Among those who have the disease, the probability that the disease will be detected by the new test is 0.7. However, the probability that the test will erroneously indicate the presence of the disease in those who do not actually have it is 0.08. It is estimated that 18 % of the population who take this test have the disease.

You may want to construct a table as in your course materials. Use a population of 10,000 people.If the test administered to an individual is positive, what is the probability that the person actually has the disease?Express your answer rounded correctly to three decimal places.

Answer 1

It is given that :

P (positive | Has disease) = 0.7

P (positive | No disease) = 0.08

P (has disease) = 0.18

P (No disease) = 1 - 0.18

= 0.82

Now if test administered to the individual is positive, the probability that the person actually have the disease is

P (Has disease | positive)
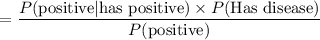`$=\frac{P(\text{positive}| \text{has positive}) * P(\text{Has disease})}{P(\text{positive})}$` ......(1)

The P(positive) is,

`$P(\text{positive}) = P(\text{positive} \cap \text{Has disease})+P(\text{positive} \cap \text{No disease})$`

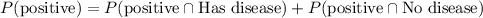
= P(positive | has disease) x P(Has disease) + P(positive | no disease) x P(No disease)

= 0.7 (0.19) + 0.04 (0.81)

= 0.1654

Now substituting the values in the equation (1), we get

P (Has disease | positive)
`$=\frac{P(\text{positive}| \text{has positive}) * P(\text{Has disease})}{P(\text{positive})}$`

`$=(0.7(0.19))/(0.1654)$`

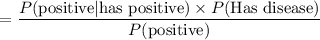
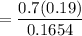
= 0.8041