Question

Segment AB has one endpoint located at A (-5, 16) and its midpoint is located at R (1, -2). What are the coordinates of endpoint B? Show all work

Answer 1

• B(7,-20).

Explanation :

we can find the co-ordinates of endpoint B using the midpoint formula which is given by

• R = (x1 + x2)/2, (y1 + y2)/2

wherein,

• R = (1,-2)
• x1 = -5
• y1 = 16

plugging in the values

• (1,-2) = (-5 + x2)/2,(16 + y2)/2

solving for x2

• (-5+x2)/2 = 1
• -5+ x2 = 2
• x2 = 2 + 5
• x2 = 7

solving for y2

• (16 +y2)/2 = -2
• 16 + y2 = -4
• y2 = -4 -16
• y2 = -20

therefore ,the co-ordinates of the endpoint B are (7,-20).

Answer 2

`\sf (7, -20)`

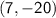
Explanation:

To find the coordinates of endpoint B, we can use the midpoint formula. The midpoint formula is given by:

`\sf \textsf{Midpoint} = \left( \frac{{x_1 + x_2}}{2}, \frac{{y_1 + y_2}}{2} \right)`

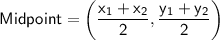
In this case, the coordinates of A are
`\sf (x_1, y_1) = (-5, 16)` and the coordinates of R (the midpoint) are
`\sf (x, y) = (1, -2)`. The coordinates of B are
`\sf (x_2, y_2)`.

Let's use the midpoint formula to solve for
`\sf (x_2, y_2)`:

`\sf (1, -2) = \left( \frac{{-5 + x_2}}{2}, \frac{{16 + y_2}}{2} \right)`

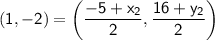
Now, we can solve for
`\sf x_2` and
`\sf y_2`:

1. Solve for
`\sf x_2`:

`\sf 1 = \frac{{-5 + x_2}}{2}`

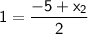
Multiply both sides by 2:

`\sf 2 = -5 + x_2`

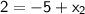
Add 5 to both sides:

`\sf x_2 = 7`

2. Solve for
`\sf y_2`:

`\sf -2 = \frac{{16 + y_2}}{2}`

Multiply both sides by 2:

`\sf -4 = 16 + y_2`

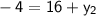
Subtract 16 from both sides:

`\sf y_2 = -20`

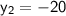
So, the coordinates of the endpoint B are
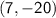`\sf (7, -20)`.