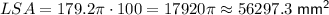Answer:
Total Surface Area = 612.2 cm³
Lateral Surface Area = 563.0 cm³
Explanation:
The formula for the surface area of a cylinder is:

Given that the diameter of a circle is twice its radius, and the diameter of the cylinder is 56 mm, then r = 28 mm.
Given that the height of the cylinder is given in centimeters, we need to convert the radius into centimeters by dividing by 10. Therefore, r = 2.8 cm.
To find the surface area of the cylinder, substitute r = 2.8 and h = 32 into the surface area formula:
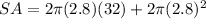
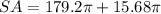
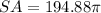
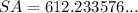
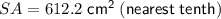
Therefore, the surface area of the cylinder is 612.2 cm², rounded to the nearest tenth.
The lateral surface area of a cylinder specifically refers to the area of the curved surface or "side" of the cylinder, excluding the areas of the circular bases:

To find the lateral surface area of the cylinder, substitute r = 2.8 and h = 32 into the LSA formula:
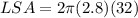
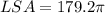
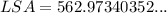
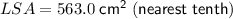
Therefore, the lateral surface area of the cylinder is 563.0 cm², rounded to the nearest tenth.

Additional Notes
If you want the areas in terms of millimeters squared, simply multiply the areas given in centimeters squared by 100: