Question

Write the explicit formula for each geometric sequence.

5, 10, 20, 40,...
10, -30, 90, -270,...
64, -32, 16, -8,...

Answer 1

see explanation

Step-by-step explanation:

the nth term (explicit formula ) for a geometric sequence is

•
`a_(n)` = a₁
`(r)^(n-1)`

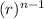
a₁ is the first term, r the common ratio , n the term number

given

5 , 10 , 20 , 40 , .............

with a₁ = 5

r is the ratio between consecutive terms , then

r =
`(a_(2) )/(a_(1) )` =
`(10)/(5)` = 2

the explicit formula is then

`a_(n)` = 5
`(2)^(n-1)`

------------------------------------------------------

given

10 , - 30 , 90 , - 270 , .......

a₁ = 10 and r =
`(a_(2) )/(a_(1) )` =
`(-30)/(10)` = - 3

the explicit formula is then

`a_(n)` = 10
`(-3)^(n-1)`

--------------------------------------------------------

given

64 , - 32 , 16 , - 8 , ............

a₁ = 64 and r =
`(a_(2) )/(a_(1) )` =
`(-32)/(64)` = -
`(1)/(2)`

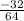the explicit formula is then

`a_(n)` = 64
`(-(1)/(2)) ^(n-1)`

--------------------------------------------------------

Answer 2

The explicit formula for a geometric sequence is an = a1 * r(n-1). The first term and common ratio are used to find the explicit formula.

Step-by-step explanation:

The explicit formula for a geometric sequence is given by the formula:

an = a1 * r(n-1)

where an is the nth term of the sequence, a1 is the first term, and r is the common ratio.

For the sequence 5, 10, 20, 40,...

The first term (a1) is 5, and the common ratio (r) is 2. Therefore, the explicit formula is:

an = 5 * 2(n-1)

For the sequence 10, -30, 90, -270,...

The first term (a1) is 10, and the common ratio (r) is -3. Therefore, the explicit formula is:

an = 10 * (-3)(n-1)

For the sequence 64, -32, 16, -8,...

The first term (a1) is 64, and the common ratio (r) is -1/2. Therefore, the explicit formula is:

an = 64 * (-1/2)(n-1)