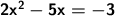
We move the expression to the left side and then change its sign.
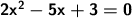
We apply the quadratic formula, and substitute.
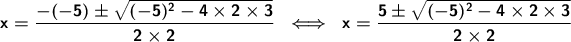
A negative number raised to the power of an even number is a positive number, so the negative sign is eliminated.

n square root of 1 is 1.


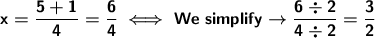
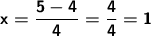
The answers are x=1, x= 3/2. Alternative B.