Question

2. By the quadratic formula, what are the solutions to the equation 2 x²-5 x=-3 ?

(A) x=4, x=6
(B) x=1, x=3/2
(c) x=-3/2, x=-1
(D) x=2, x=3

Answer 1

B

Explanation:

First we write the equation in normal form:

2 x^2 - 5x + 3 = 0

`\Delta = b^2 - 4ac = (-5)^2 - 4(2)(3) = 25 - 24 = 1`

The solutions are:

`x_(1,2) = (-b \pm √(\Delta))/(2a) = (5 \pm 1)/(4)`

x1 = (5-1)/4 = 1

x2 = (5+1)/4 = 6/4 = 3/2

Answer 2

`\boldsymbol{\sf{2x^(2) -5x=-3 }}`

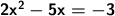
We move the expression to the left side and then change its sign.

`\boldsymbol{\sf{2x^(2) -5x+3=0 }}`

We apply the quadratic formula, and substitute.

`\boldsymbol{\sf{x=\frac{-(-5)\pm\sqrt{(-5)^(2)-4*2*3 } }{2*2} \ \iff \ x=\frac{5\pm\sqrt{(-5)^(2)-4*2*3 } }{2*2} }}`

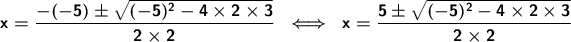
A negative number raised to the power of an even number is a positive number, so the negative sign is eliminated.

`\boldsymbol{\sf x=\frac{5\pm\sqrt{5^(2)-4*2*3 } }{2*2} \ < ==Organize \ the \ equation== > \ x=(5\pm√(1) )/(2*2) }}`

n square root of 1 is 1.

`\boldsymbol{\sf{x=(5\pm1)/(2*2) \iff \ Multiply \ x=(5\pm1)/(4)}}`

`\boldsymbol{\sf{x=(5\pm1)/(4) \iff We \ separate \ the \ answers \to \left \{ {{x=(5+1)/(4) } \atop {x=(5-1)/(4)}} \right. }}`

`\boldsymbol{\sf{x=(5+1)/(4)=(6)/(4) \iff We \ simplify \to (6/2)/(4/2)=(3)/(2) }}`

`\boldsymbol{\sf{x=(5-4)/(4)=(4)/(4)=1 }}`

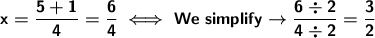
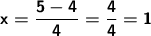
The answers are x=1, x= 3/2. Alternative B.