Question 9: The given polynomial is
 , and the roots are provided as
, and the roots are provided as
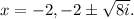
The mistake in the solution is in the synthetic division step. The correct synthetic division should be:
1 4 9 10
[-2] | -2 -4 -10
--------------------------
1 2 5 0
So, the correct quadratic equation is
 . To find the roots, you can use the quadratic formula:
. To find the roots, you can use the quadratic formula:
![\[ x = (-b \pm √(b^2 - 4ac))/(2a) \]](https://img.qammunity.org/2024/formulas/mathematics/college/n2775bpyhr6nkttp819uth89i6m8ha2p28.png)
For this equation,
 Plugging in these values:
Plugging in these values:
![\[ x = (-2 \pm √(4 - 4(1)(5)))/(2(1)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/sdcp1egx8dmx680pj68owfde5zzawp2js3.png)
![\[ x = (-2 \pm √(-16))/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1hqa7i7xxxox4ylgdyeqimre180erzffqk.png)
![\[ x = (-2 \pm 4i)/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/m0g0pv4ruij5bs9o3casizyv4e1vz295k3.png)
![\[ x = -1 \pm 2i \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/zogjz3iyg4495o0d82ueycisfhe1wavppz.png)
So, the correct roots are
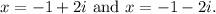
Question 10: The given solutions are
 , and the provided polynomial is
, and the provided polynomial is
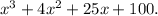
The mistake in the solution is in the factorization step. The correct factorization should be:
![\[ (x + 4)(x - 5i)(x + 5i) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/zy610w7p2j3wvsm8jx5d2w9b73e4f42avc.png)
Multiplying these factors correctly:
![\[ (x + 4)(x^2 + 25) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/vd3456jc8swnpl24lksk7prycftuq12ui9.png)
Expanding this expression gives:
![\[ x^3 + 4x^2 + 25x + 100 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/un9fccvqfvcbg7chv4yn80dp39658c081q.png)
So, the given polynomial
 is correct and matches the provided solutions. There is no mistake in this part.
is correct and matches the provided solutions. There is no mistake in this part.