Question

Find the center of the circle represented by the equation x^2-6x y^2 10y 18=0

A) (3, 5)
B) (3, -5)
C) (-3, 5)
D) (-3, -5)

Answer 1

The center of the circle represented by the equation
`x^2-6x+y^2-10y+18=0 is (3, -5).`

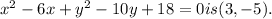
Step-by-step explanation:

The equation of the circle is x² - 6x + y² - 10y + 18 = 0. To find the center of the circle, we need to rewrite the equation in a specific form: (x - h)² + (y - k)² = r². Comparing this form to the given equation, we can identify the center as (h, k), which is the opposite sign of the coefficient of x and y. In this case, the center is (3, -5), so the correct answer is B.