Question

Consider the sequence shown.

436, 218, 109, 54.5, 27.25,...



Select the correct explicit formula for the sequence.

a
g_n=0.5·436^{(n-1)}

b
g_n=436·2^{(n-1)}

c
g_n=436·0.5^{(n-1)}

d
g_n=2·436^{(n-1)}

Answer 1

Given:

The sequence is

436, 218, 109, 54.5, 27.25,...

To find:

The explicit formula for the given sequence.

Solution:

We have,

436, 218, 109, 54.5, 27.25,...

It is a GP because the two consecutive terms have common ratio.

Here,

First term : a=436

Common ratio : d =
`(218)/(436)`

=
`(1)/(2)`

=
`0.5`

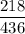
Now, the explicit formula for a GP is

`g_n=ar^((n-1))`

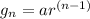
Where, a is the first term and r is the common ratio.

Putting a=436 and r=0.5, we get

`g_n=436(0.5)^((n-1))`

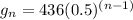
Therefore, the correct option is c.