Question

4. A group of students made a rocket and launched it vertically upwards with velocity

of 27ms^-1. What is the total distance travelled by the
rocket?

[Assume g=10ms^2]​

Answer 1

Approximately
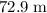`72.9\; \rm m`, assuming that the rocket had no propulsion onboard, and that air resistance on the rocket is negligible.

Step-by-step explanation:

Initial velocity of this rocket:
`u = 27\; \rm m\cdot s^(-1)`.

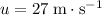When the rocket is at its maximum height, the velocity of the rocket would be equal to
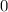`0`. That is:
`v = 0\; \rm m \cdot s^(-1)`.

The acceleration of the rocket (because of gravity) is constantly downwards, with a value of
`a = -g = -10\; \rm m \cdot s^(-2)`.

Let
`x` denote the distance that the rocket travelled from the launch site to the place where it attained maximum height. The following equation would relate
`x \!` to
`u`,
`v`, and
`a`:

`\displaystyle x = (v^2 - u^2)/(2\, a)`.

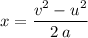Apply this equation to find the value of
`x`:

`\begin{aligned} x &= (v^2 - u^2)/(2\, a) \\ &= (\left(0\; \rm m\cdot s^(-1)\right)^(2) - \left(27\; \rm m \cdot s^(-1)\right)^(2))/(2 * 10\; \rm m \cdot s^(-2)) = 36.45\; \rm m\end{aligned}`.

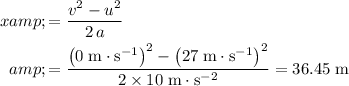In other words, the maximum height that this rocket attained would be
`36.45\; \rm m`.

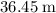Again, assume that the air resistance on this rocket is negligible. The rocket would return to the ground along the same path, and would cover a total distance of
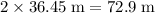`2* 36.45\; \rm m = 72.9\; \rm m`.