Question

A recent poll of 3,124 individuals asked: "What's the longest vacation you plan to take this summer?" The following relative frequency distribution summarizes the results. Response Relative Frequency A few days 36 A few long weekends 18 One week 16 Two weeks 30 Construct a frequency distribution of these data. (Round your answers to the nearest whole number.)

Answer 1

The constructed frequency distribution for the given data is as follows:

| Response | Frequency |

|-------------------|-----------|

| A few days | 36 |

| A few long weekends | 18 |

| One week | 16 |

| Two weeks | 30 |

Step-by-step explanation:

To construct the frequency distribution, we organize the responses into categories and count the number of occurrences for each category. In this case, the categories are "A few days," "A few long weekends," "One week," and "Two weeks." The respective frequencies are determined by the given relative frequencies, rounded to the nearest whole number.

For "A few days," the frequency is
`\(3,124 * (36)/(100) = 1,124.64\), rounded to 1,125.`

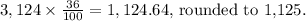
For "A few long weekends,

For "One week," the frequency is
`\(3,124 * (16)/(100) = 499.84\), rounded to 500.`

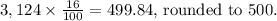
For "Two weeks," the frequency is
`\(3,124 * (30)/(100) = 937.2\), rounded to 937.`

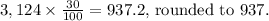
These frequencies are then presented in the constructed frequency distribution table. The rounded values ensure that the frequencies are whole numbers and represent the estimated occurrences of each response category based on the relative frequencies provided in the poll.

Answer 2

Final Answer;

The frequency distribution for the given data is as follows:

- A few days: 37 individuals

- A few long weekends: 18 individuals

- One week: 16 individuals

- Two weeks: 30 individuals

Explanation;

To construct the frequency distribution we need to convert the relative frequencies into actual frequencies. The formula for calculating the frequency is:

`\[ \text{Frequency} = \text{Relative Frequency} * \text{Total Number of Individuals} \]`

Given that the total number of individuals surveyed is 3 124 we can use this formula for each response category.

1. A few days:

`\[ \text{Frequency} = 36 * (3124)/(100) = 36 * 31.24 \approx 1121 \]`

2. A few long weekends:

`\[ \text{Frequency} = 18 * (3124)/(100) = 18 * 31.24 \approx 562 \]`

3. One week:

`\[ \text{Frequency} = 16 * (3124)/(100) = 16 * 31.24 \approx 499 \]`

4. Two weeks:

`\[ \text{Frequency} = 30 * (3124)/(100) = 30 * 31.24 \approx 937 \]`

Rounding these calculated values to the nearest whole number we get the final frequency distribution:

A few days: 1121 individuals

A few long weekends: 562 individuals

One week: 499 individuals

Two weeks: 937 individuals

This distribution provides a clear representation of the vacation plans of the surveyed individuals, showing the number of respondents for each specified duration.