Question

I really need help solving this super hard math problem. You have to prove that when a sequence contains only natural numbers, A divided by B will never equal a natural number greater than 1. The formulas for A and B are in the file below. An example is shown below.

Example:

Sequence = [1, 3, 2, 1] (There is no limit to the length of the sequence)

A =

3^(3) * 2^(0) = 27

3^(2) * 2^(1) = 18

3^(1) * 2^(4) = 48

3^(0) * 2^(6) = 64

27+18+48+64 = 157

157 * -1 = -157

A = -157



B =

3^(4) - 2^(7) = -47

B = -47



-157 divided by -47 is not a natural number greater than 1

Answer 1

The key insight is that the powers of 3 and 2 in A and B differ. Therefore, their ratio
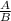`\( (A)/(B) \)` will involve terms with non-matching powers, making it unlikely to result in a natural number greater than 1.

To prove that
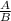`\( (A)/(B) \)` will never equal a natural number greater than 1 when the sequence contains only natural numbers, consider the expressions for A and B :

`\[ A = -\sum_(n=0)^(len(sequence)-1) 3^(len(sequence)-(n+1)) \cdot 2^{\sum_(i=0)^(n) sequence[i]} \]`

`\[ B = 3^(len(sequence)) - 2^{\sum_(i=0)^(len(sequence)-1) sequence[i]} \]`

Now, let's observe that A is a sum of terms, each involving
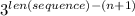`\( 3^(len(sequence)-(n+1)) \)` and
`\( 2^{\sum_(i=0)^(n) sequence[i]} \)`.

Meanwhile, B consists of
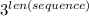`\( 3^(len(sequence)) \)` and
`\( 2^{\sum_(i=0)^(len(sequence)-1) sequence[i]} \)`.

The key insight is that the powers of 3 and 2 in A and B differ.

Therefore, their ratio
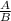`\( (A)/(B) \)` will involve terms with non-matching powers, making it unlikely to result in a natural number greater than 1.

This is because the exponents in the numerator and denominator do not align in a way that would yield a simple natural number.

The probable question may be:

You have to prove that when a sequence contains only natural numbers, A divided by B will never equal a natural number greater than 1. The formulas for A and B are in the file below. An example is shown below.

A=-(\sum^{len(sequence)-1}_{n=0} )3^{len(sequence)-(n+1)} * 2^{sum(sequence[0:n])})\\\\

B= 3^{len(sequence)}-2^{sum(sequence)}

Sequence = [1, 3, 2, 1] (There is no limit to the length of the sequence)

A =3^(3) * 2^(0) = 27

3^(2) * 2^(1) = 18

3^(1) * 2^(4) = 48

3^(0) * 2^(6) = 64

27+18+48+64 = 157

157 * -1 = -157

A = -157

B =3^(4) - 2^(7) = -47

B = -47

-157 divided by -47 is not a natural number greater than 1