Question

CALCULUS: For an object whose velocity in ft/sec is given by v(t) = sin(t), what is its distance, in feet, travelled on the interval t = 1 to t = 5?

A. 0.45
B. 2.82
C. 0.03

Answer 1

The linked answer is wrong because that integral gives you the net displacement of the object, not the total distance.

To get the distance, you have to integrate the speed (as opposed to velocity), which involves integrating the absolute value of the velocity function.

`\mathrm{distance} = \displaystyle\int_1^5 |\sin(t)| \,\mathrm dt`

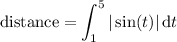
By definition of absolute value,

`|\sin(t)|=\begin{cases}\sin(t)&\text{for }\sin(t)\ge0\\-\sin(t)&\text{for }\sin(t)<0\end{cases}`

Over this particular integration interval,

• sin(t ) ≥ 0 for 1 ≤ t < π, and

• sin(t ) < 0 for π < t ≤ 5

so you end up splitting the integral at t = π as

`\mathrm{distance} = \displaystyle\int_1^\pi \sin(t)\,\mathrm dt + \int_\pi^5 (-\sin(t))\,\mathrm dt`

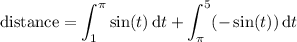
Now compute the distance:

`\mathrm{distance} = -\cos(t)\bigg|_1^\pi + \cos(t)\bigg|_\pi^5`

`\mathrm{distance} = -(\cos(\pi) - \cos(1)) + (\cos(5) - \cos(\pi))`

`\mathrm{distance} = -2\cos(\pi) + \cos(1) + \cos(5) \approx 2.82`

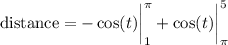
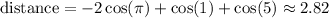
making B the correct answer.