The difference between the compound interest on a sum of Rs. 25,000 for 3 years at a rate of 4% per annum would be approximately Rs. 3,121.60.
How to calculate the compound interest
To calculate the compound interest on a sum of Rs. 25,000 for 3 years at a rate of 4% per annum, use the following formula for compound interest:
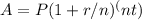
Where:
A = Final amount (including interest)
P = Principal amount (initial sum)
r = Annual interest rate (in decimal form)
n = Number of times interest is compounded per year
t = Number of years
In this case, the principal amount (P) is Rs. 25,000, the annual interest rate (r) is 4% or 0.04, and the time period (t) is 3 years.
Let's assume the interest is compounded annually (n = 1).
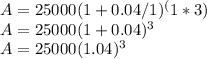
A = 25000(1.124864)
A ≈ 28121.60
The final amount (A) after 3 years would be approximately Rs. 28,121.60.
To find the compound interest, subtract the principal amount from the final amount:
Compound Interest = A - P
Compound Interest = 28121.60 - 25000
Compound Interest ≈ Rs. 3,121.60
Therefore, the difference between the compound interest on a sum of Rs. 25,000 for 3 years at a rate of 4% per annum would be approximately Rs. 3,121.60.