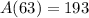Answer:
193 gallons
Explanation:
Given
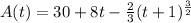
Required
Determine the maximum amount of water the tank can hold --- Missing from the question
Start by differentiating A w.r.t t
![A'(t) = 0 + 8 + (d)/(dt)[-(2)/(3)(t+1)^{(3)/(2)}]](https://img.qammunity.org/2022/formulas/mathematics/high-school/v14bf7a6sjfqkihg1vc4n0qair09i0qsm9.png)
Solving:
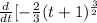
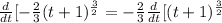
Apply power rule:
![(d)/(dt)[-(2)/(3)(t+1)^{(3)/(2)} = -(2)/(3)[(3)/(2)(t + 1)^{(3)/(2)-1} * (d)/(dt)[t+1]](https://img.qammunity.org/2022/formulas/mathematics/high-school/3sbzdnwwty3tg6y9vw87atex35rixrimp6.png)
![(d)/(dt)[-(2)/(3)(t+1)^{(3)/(2)} = -(t + 1)^{(3)/(2)-1} * (d)/(dt)[t+1]](https://img.qammunity.org/2022/formulas/mathematics/high-school/s1t527myzkx2xp6quq6ugpz0eagm1si4iq.png)
![(d)/(dt)[-(2)/(3)(t+1)^{(3)/(2)} = -(t + 1)^{(3)/(2)-1} * [1+0]](https://img.qammunity.org/2022/formulas/mathematics/high-school/b5fcrjqn8uw3pmsqzld1lkeojblv6e2zf5.png)
![(d)/(dt)[-(2)/(3)(t+1)^{(3)/(2)} = -(t + 1)^{(3)/(2)-1} * [1]](https://img.qammunity.org/2022/formulas/mathematics/high-school/pq55sfhsdupwagmge1zqrblp63oju2xx0u.png)
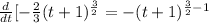
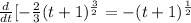
So:
![A'(t) = 0 + 8 + (d)/(dt)[-(2)/(3)(t+1)^{(3)/(2)}]](https://img.qammunity.org/2022/formulas/mathematics/high-school/v14bf7a6sjfqkihg1vc4n0qair09i0qsm9.png)
A'(t) = 0 + 8 + \frac{d}{dt}[-\frac{2}{3}(t+1)^{\frac{3}{2}}]
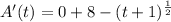
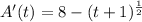
Equate to 0 to solve for t
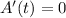
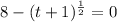
Collect Like Term
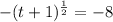
Square both sides
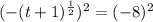
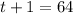
Make t the subject:
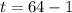

So, the tank is at maximum when t = 63.
Substitute 63 for t in:
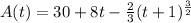
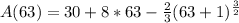
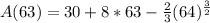
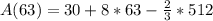
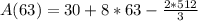
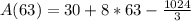
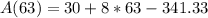
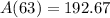
Approximate: