Question

I Will give an expert or whoever knows how to do this 100 points. Can you help me Please!!!!! Pls don't take my points without doing the assignment right.Thank you !!!

Read the instructions carefully!!!!

Answer 1

I will do the first example, by explaining how to graph it. Then you can do the second example.

`f(x) = x^3-10x^2+28x-24`

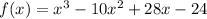
We start by determining the the x-intercepts, by letting y = 0:

`x^3-10x^2+28x-24=0,\\\left(x-2\right)^2\left(x-6\right)=0,\\x=2,\:x=6`

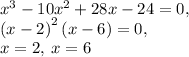
The x-intercepts of the graph are (2, 0) and (6, 0) respectively. Now we determine the y-intercepts by letting x = 0:

`f\left(x\right)=\left(0\right)^3-10\left(0\right)^2+28\left(0\right)-24 = - 24`

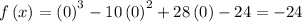
So the y-intercept is (0, -24). But remember we need one more point, as there has to be a transition between the x-intercepts. This is the minimum of the graph. To determine this, we take the derivative of the function, and then equate it to 0 to find the "critical points." :

`(d)/(dx)\left(x^3-10x^2+28x-24\right)\\\\ =>(d)/(dx)\left(x^3\right)-(d)/(dx)\left(10x^2\right)+(d)/(dx)\left(28x\right)-(d)/(dx)\left(24\right)\\\\=> 3x^2-20x+28-0\\=> 3x^2-20x+28`

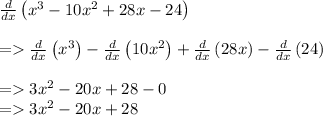
Now we equate this to 0, and apply the quadratic equation. In this case we can actually factor it :

`3x^2-20x+28=0,\\\left(x-2\right)\left(3x-14\right)=0,\\\\x=2,\:x=(14)/(3)`

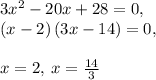
x = 2 is our maximum, or our x-intercept (2, 0). Therefore we have to take 14/3 as our minimum, and determine the y-value:

`f\left(x\right)=\left((14)/(3)\right)^3-10\left((14)/(3)\right)^2+28\left((14)/(3)\right)-24\\\\= -(256)/(27)`

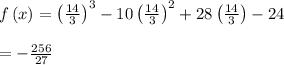
Minimum: (14/3, -256/27)

Graph is in the attachment below -