I will do the first example, by explaining how to graph it. Then you can do the second example.
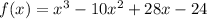
We start by determining the the x-intercepts, by letting y = 0:
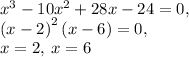
The x-intercepts of the graph are (2, 0) and (6, 0) respectively. Now we determine the y-intercepts by letting x = 0:
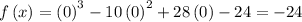
So the y-intercept is (0, -24). But remember we need one more point, as there has to be a transition between the x-intercepts. This is the minimum of the graph. To determine this, we take the derivative of the function, and then equate it to 0 to find the "critical points." :
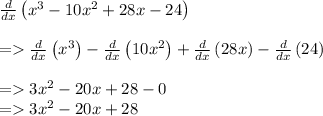
Now we equate this to 0, and apply the quadratic equation. In this case we can actually factor it :
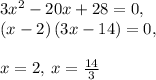
x = 2 is our maximum, or our x-intercept (2, 0). Therefore we have to take 14/3 as our minimum, and determine the y-value:
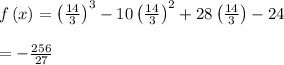
Minimum: (14/3, -256/27)
Graph is in the attachment below -