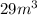The total volume of the greenhouse, rounded to the nearest cubic meter, is 29 cubic meters.
V=
To solve the volume of the greenhouse depicted in the image, we need to consider it as a combination of simple geometric shapes and calculate the volume of each, then sum them up.
The greenhouse can be divided into three parts:
1. A rectangular prism (the base part):
- Length (l) = 13 m
- Width (w) = 0.8 m
- Height (h1) = 0.8 m
2. A cuboid (the middle part):
- Length (l) = 13 m
- Width (w) = 0.8 m
- Height (h2) = 1.6 m
3. A triangular prism (the top part):
- Base length (b) = 13 m
- Width (w) = 0.8 m
- Height (h3) = 0.8 m
The volume of the greenhouse,
 , is the sum of the volumes of these parts:
, is the sum of the volumes of these parts:
Volume of the rectangular prism:
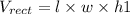
Volume of the cuboid:
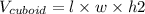
Volume of the triangular prism:
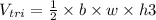
So, the total volume is:

Now, we can calculate each part:

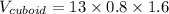
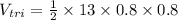
The total volume of the greenhouse, rounded to the nearest cubic meter, is 29 cubic meters.
V=