Given:
The bases of a trapezoid lie on the lines
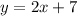
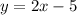
To find:
The equation that contains the midsegment of the trapezoid.
Solution:
The slope intercept form of a line is

Where, m is slope and b is y-intercept.
On comparing
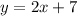 with slope intercept form, we get
with slope intercept form, we get
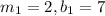
On comparing
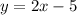 with slope intercept form, we get
with slope intercept form, we get
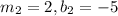
The slope of parallel lines are equal and midsegment of a trapezoid is parallel to the bases. So, the slope of the bases line and the midsegment line are equal.
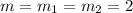
The y-intercept of one base is 7 and y-intercept of second base is -5. The y-intercept of the midsegment is equal to the average of y-intersects of the bases.
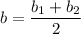
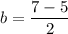
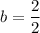
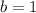
So, the y-intercept of the required line is 1.
Putting m=2 and b=1 in slope intercept form, we get
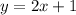
Therefore, the equation of line that contains the midsegment of the trapezoid is
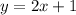 .
.