Question

The acceleration of an object is =4 m/s^2.?

The acceleration of an object is =4 m/s^2. Find the distance of the object from the origin under the initial conditions (0)=9 m, (0)=16 m/s.

(Use symbolic notation and fractions where needed.)

Answer 1

`\displaystyle s(t) = (2t^3)/(3) + 16t + 9`

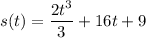
General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Calculus

Antiderivatives - Integrals

Integration Constant C

Integration Rule [Reverse Power Rule]:
`\displaystyle \int {x^n} \, dx = (x^(n + 1))/(n + 1) + C`

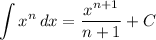
Integration Property [Multiplied Constant]:
`\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx`

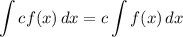
Integration Property [Addition/Subtraction]:
`\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx`

Explanation:

*Note:

Velocity is the derivative of Position, and Acceleration is derivative of Velocity.

↓

Velocity is integration of Acceleration, Position is integration of Velocity.

Step 1: Define

a(t) = 4t m/s²

s(0) = 9 m

v(0) = 16 m/s

Step 2: Find Velocity Function

Integration Pt. 1

1. [Velocity] Set up integral:
   `\displaystyle v(t) = \int {a(t)} \, dt`
2. [Velocity] Substitute in function:
   `\displaystyle v(t) = \int {4t} \, dt`
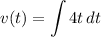
3. [Velocity] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle v(t) = 4\int {t} \, dt`
4. [Velocity] Integrate [Integration Rule - Reverse Power Rule]:
   `\displaystyle v(t) = 4((t^2)/(2)) + C`
5. [Velocity] Multiply:
   `\displaystyle v(t) = 2t^2 + C`

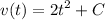
Finding C

1. [Velocity] Substitute in initial condition:
   `\displaystyle v(0) = 2(0)^2 + C`
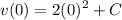
2. [Velocity] Substitute in function value:
   `\displaystyle 16 = 2(0)^2 + C`
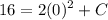
3. [Velocity] Evaluate exponents:
   `\displaystyle 16 = 2(0) + C`
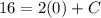
4. [Velocity] Multiply:
   `\displaystyle 16 = C`
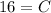
5. Rewrite:
   `\displaystyle C = 16`

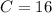
Velocity Function:
`\displaystyle v(t) = 2t^2 + 16`

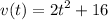
Step 3: Find Position Function

Integration Pt. 2

1. [Position] Set up integral:
   `\displaystyle s(t) = \int {v(t)} \, dt`
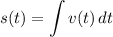
2. [Position] Substitute in function:
   `\displaystyle s(t) = \int {2t^2 + 16} \, dt`
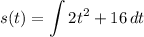
3. [Position] Rewrite [Integration Property - Addition]:
   `\displaystyle s(t) = \int {2t^2} \, dt + \int {16} \, dt`
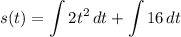
4. [Position] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle s(t) = 2\int {t^2} \, dt + 16\int {} \, dt`
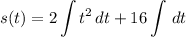
5. [Position] Integrate [Integration Rule - Reverse Power Rule]:
   `\displaystyle s(t) = 2((t^3)/(3)) + 16t + C`
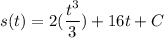
6. [Position] Multiply:
   `\displaystyle s(t) = (2t^3)/(3) + 16t + C`

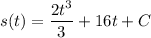
Finding C

1. [Position] Substitute in initial condition:
   `\displaystyle s(0) = (2(0)^3)/(3) + 16(0) + C`
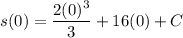
2. [Position] Substitute in function value:
   `\displaystyle 9 = (2(0)^3)/(3) + 16(0) + C`
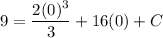
3. [Position] Evaluate exponents:
   `\displaystyle 9 = (2(0))/(3) + 16(0) + C`
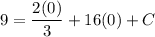
4. [Position] Multiply:
   `\displaystyle 9 = (0)/(3) + C`
5. [Position] Divide:
   `\displaystyle 9 = C`
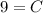
6. [Position] Rewrite:
   `\displaystyle C = 9`

Position Function:
`\displaystyle s(t) = (2t^3)/(3) + 16t + 9`

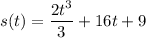
Topic: AP Calculus AB/BC (Calculus I/II)

Unit: Integration

Book: College Calculus 10e