Question

≠A student took a system of equations, multiplied the first equation by and the second equation by , then added the results together. Based on this, she concluded that there were no solutions. Which system of equations could she have started with?

Answer 1

C. 3x+6y=9 and-2x-4y=4

Explanation:

Given

Steps:

• Multiply equation 1 by 2

• Multiply equation 2 by 3

• Add the results together

The attachment completes the question

(a): -2x+4y=4 and -3x+6y=6

Multiply by 2:
`-2x+4y=4 ===> -4x + 8y = 4`

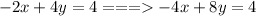
Multiply by 3:
`-3x+6y=6 ===> -6x + 12y = 12`

Add together

`-4x - 6x + 8y + 12y = 4 + 12`

`-10x + 20y = 16`

B. 3x+y=12 and -3x+6y=6

Multiply by 2:
`3x+y=12 ===> 6x + 2y = 24`

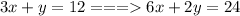
Multiply by 3:
`-3x+6y=6 ==> -9x + 18y = 18`

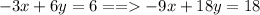
Add together:

`6x - 9x + 2y + 18y = 24 + 18`

`-3y + 10y = 42`

C. 3x+6y=9 and-2x-4y=4

Multiply by 2:
`3x+6y=9 ===>6x + 12y = 18`

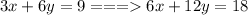
Multiply by 3:
`-2x-4y=4 ===> -6x - 12y = 12`

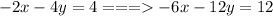
Add together:

`6x - 6x + 12y - 12y = 18 + 12`

`0 = 30`

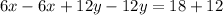
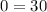
This is the equation the student could have used because 0 = 30 means the equation has no solution.