Final answer:
The pattern of the sequence -1, 0, 3, 8, 15,... is explained by (b) Squaring consecutive odd numbers.
Step-by-step explanation:
The sequence follows the pattern of squaring consecutive odd numbers. Starting with the first term
 equals 1, the second term
equals 1, the second term
 equals 0, the third term is
equals 0, the third term is
 which equals 9, the fourth term is
which equals 9, the fourth term is
 which equals 16, and so on. Each term in the sequence is obtained by squaring the consecutive odd numbers and subtracting 1. The general form of the pattern is
which equals 16, and so on. Each term in the sequence is obtained by squaring the consecutive odd numbers and subtracting 1. The general form of the pattern is
 , where n represents consecutive odd numbers.
, where n represents consecutive odd numbers.
For example:
- First term:
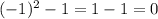
- Second term:
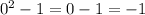
- Third term:

- Fourth term:
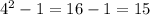
The next two terms in the sequence would be obtained by squaring the next consecutive odd numbers in the pattern:
 and
and
 . Therefore, the correct explanation for the pattern and the conjecture about the next two terms are based on squaring consecutive odd numbers.
. Therefore, the correct explanation for the pattern and the conjecture about the next two terms are based on squaring consecutive odd numbers.