Question

Mike and Emily each have invested $100,000 in an investment account. No other contributions will be made to their investment account. Both have the same goal; they each want their account to reach $3,000,000 at which time each will retire. Mike has his money invested in risk-free securities with an expected return of 12% compounded monthly. Emily has her money invested in a stock fund with an expected return of 15% compounded quarterly. How many years after Emily retires will Mike retire? (6 marks)

Answer 1

By applying the compound interest formula, we can find that Emily will retire after approximately 16.2 years and Mike will retire after approximately 19.7 years. Therefore, Mike will retire around 3.5 years after Emily does.

Step-by-step explanation:

The question asks how many years after Emily retires will Mike retire, given the amounts they have invested and their respective rates of compound interest. To solve this problem, we will use the compound interest formula A = P(1 + r/n)^(nt), where A is the amount of money accumulated after n years, including interest, P is the principal amount (the initial sum of money), r is the annual interest rate (decimal), n is the number of times that interest is compounded per unit t, and t is the time the money is invested for in years.

First, we'll calculate the number of years it will take for Emily's investment to grow to $3,000,000 with her annual return of 15% compounded quarterly:

`3000000 = 100000(1 + 0.15/4)^(4t)`

`30 = (1 + 0.0375)^(4t)`

`(1 + 0.0375)^(4t) = 30`
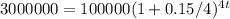
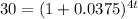
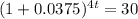
4t*log(1.0375) = log(30)
t = log(30) / (4*log(1.0375))
t is approximately 16.2 years.

Then, we'll calculate the number of years it will take for Mike's investment to grow to $3,000,000 with his annual return of 12% compounded monthly:

`3000000 = 100000(1 + 0.12/12)^(12t)`

`30 = (1 + 0.01)^(12t)`

`(1 + 0.01)^(12t) = 30`
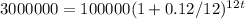
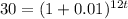
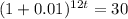
12t*log(1.01) = log(30)
t = log(30) / (12*log(1.01))
t is approximately 19.7 years.

Subtracting Emily's time from Mike's time gives us the number of years Mike retires after Emily:

19.7 - 16.2 = 3.5 years

Therefore, Mike will retire approximately 3.5 years after Emily.

Answer 2

Mike will retire approximately 23.83 years after Emily retires.

Step-by-step explanation: