Explanation:
First we must calculate the interquartile range (IQR), using this equation:
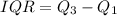
Based on the information provided we fill in:
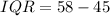
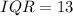
In order to find what the range for the data set is we need to use the Interquartile Rule:
 ×
×
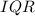
 ×
×
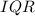
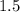 ×
×
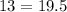
Now we plugin in:
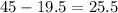
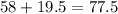
Any number below 25.5 is a possible outlier and any number above 77.5 is a possible outlier.
Answer:
Based on the results of the calculations, 25 could be a possible outlier in the data set.