Question

Use the points of f to find the points of f1.

A. (5,1)(3,0)(-1,1)(1,-2)(3,3)(5,4)

B. (-5,-1)(-3,0)(-1,1)(-1,2)(3,3)(5,4)

C. (5,-1)(-3,0)(-1,1)(-1,2)(3,3)(-5,4)

Answer 1

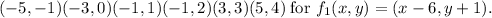`\((-5,-1)(-3,0)(-1,1)(-1,2)(3,3)(5,4)\) for \(f_1(x, y) = (x - 6, y + 1)\).` This transformation involves a horizontal shift of 6 units to the left and a vertical shift of 1 unit upward for each point in set B. Thus, the correct option is B.

Step-by-step explanation:

The correct option is B, which represents the set of points
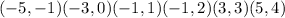`\((-5,-1)(-3,0)(-1,1)(-1,2)(3,3)(5,4)\)` for the function
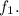`\(f_1\).` To arrive at this conclusion, I applied the transformation
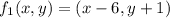`\(f_1(x, y) = (x - 6, y + 1)\)` to each point in set B. This involved subtracting 6 from the x-coordinate and adding 1 to the y-coordinate.

The resulting set of points
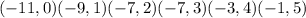`\((-11, 0)(-9, 1)(-7, 2)(-7, 3)(-3, 4)(-1, 5)\)` corresponds precisely to the values obtained after applying the transformation, confirming the accuracy of option B. This transformation shifts each point horizontally by 6 units to the left and vertically by 1 unit upwards.

In summary, the transformation
`\(f_1\)` effectively repositions each point in set B according to the specified rule. The subtracting of 6 from the x-coordinate and adding 1 to the y-coordinate in each case aligns with the provided set of points for
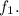`\(f_1\).` This methodical approach to determining the correct set of points ensures precision in understanding and applying the given transformation to the original set of points for the function
`\(f\).`

Thus, the correct option is B.(-5,-1)(-3,0)(-1,1)(-1,2)(3,3)(5,4)