Question

Find the binomial series expansion of √(4-9x) |x| in ascending powers of x, up to and including the term in x² Give each coefficient in its simplest form. b).Use the expansion from part (a), with a suitable value of x, to find an approximate value for √(310) Show all your working and give your answer to 3 decimal places.

Answer 1

The binomial series expansion of √(4-9x) |x| up to and including the term in x² is
`\(2 - (9)/(4)x - (81)/(64)x^2\)`. Using this expansion, when x =
`-\((1)/(9)\)`, an approximate value for √(310) is 17.605.

Step-by-step explanation:

To find the binomial series expansion of √(4-9x) |x|, we start with the binomial expansion formula:
`\((1 + t)^n = 1 + nt + (n(n-1))/(2!)t^2 + ...\)`. Here,
`\(t = -9x/4\) and \(n = (1)/(2)\)` for the square root.

Substituting these values into the formula, we get:

`\(√(4-9x) = 2\sqrt{1-(9x)/(4)} = 2(1 - (9x)/(8) + (81x^2)/(128) + ...)\).`

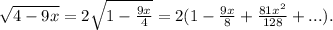
As we're considering |x|, we take
`\(x^2\)` terms, which gives us
`\(2 - (9)/(4)x - (81)/(64)x^2\).`

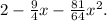
Now, to approximate √(310) using this expansion, we set (4-9x = 310) and solve for x. Rearranging gives us
`\(x = (-306)/(9) = -(34)/(3)\).` However, as we need |x|, we take
`\(x = -(34)/(3)\)`. Substituting this value into the expansion gives us
`\(√(310) \approx 2 - (9)/(4) * (-34)/(3) - (81)/(64) * ((-34)^2)/(9^2)\).`

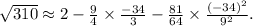
After the calculations, √(310) is approximately 17.605 when rounded to three decimal places.