The given expressions result in the following simplified values: (a)
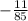 , (b)
, (b)
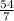 , (c)
, (c)
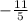 , (d)
, (d)
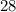 , (e)
, (e)
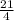 , (f) (7), (g) (0), (h)
, (f) (7), (g) (0), (h)
 , (i)
, (i)
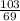 .
.
Let's address each subtraction and simplification:
(a)
 : To subtract these fractions, find a common denominator, which is 85. Then, subtract the numerators:
: To subtract these fractions, find a common denominator, which is 85. Then, subtract the numerators:
![\[ (42)/(17) - (13)/(5) = (42 \cdot 5 - 13 \cdot 17)/(17 \cdot 5) = (210 - 221)/(85) = -(11)/(85). \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/x11ca9r9ap1oubzlfyexnbo74j0vjt5kry.png)
(b)
 : Convert 16 to an equivalent fraction with denominator 7:
: Convert 16 to an equivalent fraction with denominator 7:
![\[ (112)/(7) - (58)/(7) = (54)/(7). \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/asml35ikx4nrv34ti85wqsbow6mksdpzu6.png)
(c)
 : Find a common denominator, which is 5:
: Find a common denominator, which is 5:
![\[ (4)/(5) - (15)/(5) = -(11)/(5). \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/nawpy0vzc2gqi8eurf8hll3ekmbb9ax4zf.png)
(d)
 : Convert 34 to an equivalent fraction with denominator 1:
: Convert 34 to an equivalent fraction with denominator 1:
![\[ (34)/(1) - (6)/(1) = (28)/(1) = 28. \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/eybuvl3ovfpagmlgn39yja1jwwz1fr4re2.png)
(e)
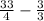 : Find a common denominator, which is 4:
: Find a common denominator, which is 4:
![\[ (33)/(4) - (12)/(4) = (21)/(4). \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/lor136jo0rd2bu5dj4p0u5rgkr3wbv4ge2.png)
(f)
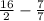 : Simplify the fractions:
: Simplify the fractions:
![\[ 8 - 1 = 7. \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/rwoswgpz3b33i5jbc03ipu2c1skicmqvjt.png)
(g)
 : Find a common denominator, which is 6:
: Find a common denominator, which is 6:
![\[ (3)/(6) - (3)/(6) = 0. \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/dkx7n8kornyuxyxgdqfdtcalvxzjtjt9o3.png)
(h)
 : Find a common denominator, which is 20:
: Find a common denominator, which is 20:
![\[ (4)/(20) - (100)/(20) = -(96)/(20) = -(24)/(5). \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1ie4r8l6c4pvdcxib94xz0aw8wpy9cqoaf.png)
(i)
 : This fraction is already in its simplest form.
: This fraction is already in its simplest form.