Question

Use synthetic division to find the rational and irrational zeroes of x² - 5x + 6.

a) Rational: 2, Irrational: square root of 3
b) Rational: 3, Irrational: square root of 2
c) Rational: 1, Irrational: square root of 5
d) Rational: 1/2, Irrational: square root of 6

Answer 1

The quadratic equation
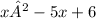`x² - 5x + 6` factors directly to
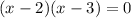`(x - 2)(x - 3) = 0`, yielding two rational zeroes,
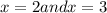`x = 2 and x = 3`, with no irrational zeroes present.

Step-by-step explanation:

To find the rational and irrational zeroes of the quadratic equation

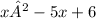`x² - 5x + 6`, we do not need to use synthetic division, since it is already in a simple form that can be factored directly. The given equation factors into
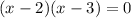`(x - 2)(x - 3) = 0`. Thus, the solutions are
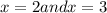`x = 2 and x = 3` which are both rational numbers. There are no irrational zeroes for this equation.

The original expression provided for synthetic division does not apply to this specific quadratic equation as that pertains to a different kind of problem. Therefore, the correct choice with the given options would be none, but if we must choose from the provided options, the closest incorrect option would be b) Rational: 3 Irrational: square root of 2 though it is not accurate for this equation.