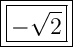Question

3. Find the value of sec 0 for the following angle:

3pi/4

Whole question is in the picture.

Answer 1

`-√(2)`

Explanation:

To find the value of sec θ, we can use the reciprocal relationship between secant and cosine.

The secant of an angle is the reciprocal of its cosine:

`\sec \theta=(1)/(\cos \theta)`

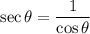
So, we can find sec(3π/4) by taking the reciprocal of the cosine of 3π/4.

According to the unit circle, the cosine of 3π/4 is:

`\cos \left((3\pi)/(4)\right)=-(√(2))/(2)`

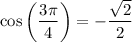
Therefore:

`\begin{aligned}\sec \left((3\pi)/(4)\right)&=(1)/(\cos\left((3\pi)/(4)\right))\\\\&=(1)/(-(√(2))/(2))\\\\&=-(2)/(√(2))\\\\&=-(2\cdot √(2))/(√(2)\cdot√(2))\\\\&=-(2√(2))/(2)\\\\&=-√(2)\end{aligned}`

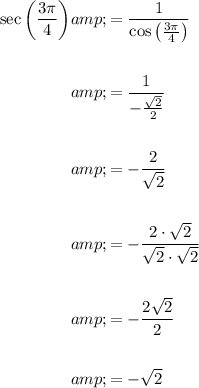
So, the value of sec θ, when the angle is 3π/4 is:

`\Large\boxed{\boxed{-√(2)}}`