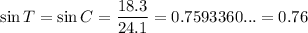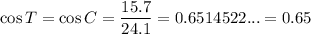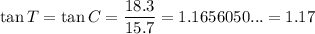Question

HELP IM STUCK!!! BEGGING.

In the figure below, (triangle) B C A ~ (triangle) S T R. Find cos T, sin T, and tan T. Round your answers to the nearest hundredth.

Answer 1

sin T = 0.76

cos T = 0.65

tan T = 1.17

Explanation:

In similar triangles, corresponding angles have the same measure, and corresponding sides are always in the same ratio.

If ΔBCA ~ ΔSTR, then m∠C = m∠T. Therefore:

`\sin T = \sin C`

`\cos T = \cos C`

`\tan T = \tan C`

To find the sine, cosine and tangent of an angle, we can use the trigonometric ratios:

`\boxed{\begin{array}{l}\underline{\sf Trigonometric\;ratios}\\\\\sf \sin(\theta)=(O)/(H)\qquad\cos(\theta)=(A)/(H)\qquad\tan(\theta)=(O)/(A)\\\\\textsf{where:}\\\phantom{ww}\bullet\;\textsf{$\theta$ is the angle.}\\\phantom{ww}\bullet\;\textsf{O is the side opposite the angle.}\\\phantom{ww}\bullet\;\textsf{A is the side adjacent the angle.}\\\phantom{ww}\bullet\;\textsf{H is the hypotenuse (the side opposite the right angle).}\end{array}}`

In the case angle C of triangle BCA:

• θ = C
• O = BA = 18.3
• A = CA = 15.7
• H = BC = 24.1

Substitute these values into the trigonometric ratios:

`\sin T=\sin C = (18.3)/(24.1)=0.7593360...=0.76`

`\cos T=\cos C = (15.7)/(24.1)=0.6514522...=0.65`

`\tan T=\tan C = (18.3)/(15.7)=1.1656050...=1.17`