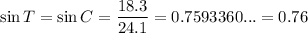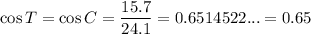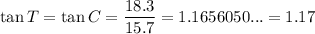Answer:
sin T = 0.76
cos T = 0.65
tan T = 1.17
Explanation:
In similar triangles, corresponding angles have the same measure, and corresponding sides are always in the same ratio.
If ΔBCA ~ ΔSTR, then m∠C = m∠T. Therefore:
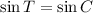
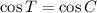
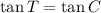
To find the sine, cosine and tangent of an angle, we can use the trigonometric ratios:

In the case angle C of triangle BCA:
- θ = C
- O = BA = 18.3
- A = CA = 15.7
- H = BC = 24.1
Substitute these values into the trigonometric ratios: