Question

The function f is given by f(x)=log base 3 of x. Which of the following could be the graph of y=f^-1 (x)

Answer 1

Graph C

Step-by-step explanation:

Given logarithmic function:

`f(x)=\log_3(x)`

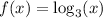
The graph of the inverse of the given function is its reflection in the line y = x. Therefore, to determine the graph of the inverse function f⁻¹(x), we first need to clarify the behaviour of the original function f(x).

For a logarithmic function to be defined, its argument must be positive. This means that the domain of f(x) is (0, ∞), and so the graph of f(x) does not have a y-intercept.

The x-intercept can be found by setting the function to zero and solving for x, so the graph of f(x) crosses the x-axis at (1, 0).

Applying the rule logₐ(a) = 1, a point on the curve of f(x) is (3, 1).

The end behaviours of the graph of f(x) are:

• As x approaches 0 from the positive side, f(x) approaches -∞.
• As x approaches +∞, f(x) approaches +∞.

Therefore, the curve begins in quadrant IV, crosses the x-axis at x = 1, and continues in quadrant I.

With this information, we can now describe the characteristics of the graph of f⁻¹(x):

• The graph will not cross the x-axis because the original function f(x) does not have a y-intercept.
• It will cross the y-axis at (0, 1) because f(1) = 0 is reflected across the line y = x to become f⁻¹(0) = 1.
• It will pass through the point (1, 3) because f(3) = 1 is reflected across the line y = x to become f⁻¹(1) = 3.
• The graph will begin in quadrant II, reflecting the behavior of f(x) beginning in quadrant IV.

Therefore, the graph that is the graph of f⁻¹(x) is:

`\Large\boxed{\boxed{\sf Graph\;C}}`