Answer:

Explanation:
We can either Sine ratio or cosine ratio to find the value of x in right angled triangle.
If we use sine ratio
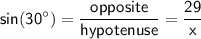
Solve for x.
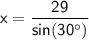
Substitute the value of sin(30°) = ½
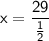
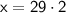
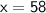
If we use cosine ratio
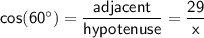
Solve for x.
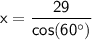
Substitute the value of cos(60°) = ½
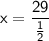
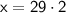
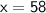
So, the value of x is 58.