The direction of the probe's final velocity is approximately
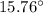 with respect to the x-axis.
with respect to the x-axis.
To solve this problem, we can use the principles of conservation of linear momentum and conservation of kinetic energy. The linear momentum of the system (probe + asteroid) is conserved in the absence of external forces, and the kinetic energy is conserved if the collision is elastic.
Let's denote:
-
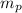 : mass of the probe (500 kg)
: mass of the probe (500 kg)
-
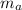 : mass of the asteroid (2000 kg)
: mass of the asteroid (2000 kg)
-
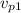 : initial velocity of the probe (400 m/s)
: initial velocity of the probe (400 m/s)
-
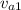 : initial velocity of the asteroid (100 m/s)
: initial velocity of the asteroid (100 m/s)
-
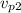 : final velocity of the probe (300 m/s)
: final velocity of the probe (300 m/s)
-
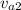 : final velocity of the asteroid (165 m/s)
: final velocity of the asteroid (165 m/s)
The linear momentum before the collision is the sum of the linear momentum of the probe and the asteroid:
![\[m_p \cdot v_(p1) + m_a \cdot v_(a1)\]](https://img.qammunity.org/2024/formulas/physics/high-school/wrnhy9jn4d5hldcmwbajlg9dz03vk72zjk.png)
The linear momentum after the collision is the sum of the linear momentum of the probe and the asteroid in their final states:
![\[m_p \cdot v_(p2) + m_a \cdot v_(a2)\]](https://img.qammunity.org/2024/formulas/physics/high-school/sh1ggni9snczxlkn8vaoujq8x1wwj4dnay.png)
Now, we can set up an equation using the conservation of linear momentum:
![\[m_p \cdot v_(p1) + m_a \cdot v_(a1) = m_p \cdot v_(p2) + m_a \cdot v_(a2)\]](https://img.qammunity.org/2024/formulas/physics/high-school/8fhxt0b0kfnsmtigy2n8ck1goubbppv036.png)
Plug in the known values:
![\[(500 \, \text{kg} \cdot 400 \, \text{m/s}) + (2000 \, \text{kg} \cdot 100 \, \text{m/s}) = (500 \, \text{kg} \cdot 300 \, \text{m/s}) + (2000 \, \text{kg} \cdot 165 \, \text{m/s})\]](https://img.qammunity.org/2024/formulas/physics/high-school/xyru56x6wa2d41fr4kucs4sfq5lk0xbjx1.png)
Now, solve for \(v_{a2}\) (final velocity of the asteroid):
![\[(200000 \, \text{kg} \cdot \text{m/s}) + (200000 \, \text{kg} \cdot \text{m/s}) = (150000 \, \text{kg} \cdot \text{m/s}) + (330000 \, \text{kg} \cdot \text{m/s})\]](https://img.qammunity.org/2024/formulas/physics/high-school/555s2yekczzb1zdif05d3gefoc7h7ja91x.png)
![\[400000 \, \text{kg} \cdot \text{m/s} = 480000 \, \text{kg} \cdot \text{m/s}\]](https://img.qammunity.org/2024/formulas/physics/high-school/p7e87csm68cuhwdpif6a5d8adk0xmkgpvx.png)
This implies that the final velocity of the asteroid
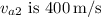 .
.
Now, we can use trigonometry to find the direction of the final velocity of the probe. The angle \(\theta\) between the initial velocity of the asteroid and its final velocity is given as \(71^\circ\).
![\[\tan(\theta) = \frac{{v_(a2y)}}{{v_(a1)}}\]](https://img.qammunity.org/2024/formulas/physics/high-school/n81nejrpx6bdnvznlmytrdd8ijaw9t8lpg.png)
where
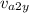 is the component of the final velocity of the asteroid in the y-direction.
is the component of the final velocity of the asteroid in the y-direction.
![\[\tan(71^\circ) = \frac{{v_(a2y)}}{{100 \, \text{m/s}}}\]](https://img.qammunity.org/2024/formulas/physics/high-school/5hofm8zq1gl1dvxfq397v2hu3tdzizsk9v.png)
Solve for
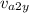 :
:
![\[v_(a2y) = 100 \, \text{m/s} \cdot \tan(71^\circ)\]](https://img.qammunity.org/2024/formulas/physics/high-school/z5vdoij1xeenwlnz6i62ikxbcw4pb6wzpx.png)
Now, we can find the component of the final velocity of the probe in the y-direction
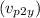 :
:
![\[v_(p2y) = v_(p2) \cdot \sin(\theta)\]](https://img.qammunity.org/2024/formulas/physics/high-school/xkjmyox956qx3nm4ww0ez2fwng3zsc53af.png)
Substitute the values:
![\[v_(p2y) = 300 \, \text{m/s} \cdot \sin(71^\circ)\]](https://img.qammunity.org/2024/formulas/physics/high-school/sh1twof2xm0f95pcxcgfg7wgfkm0oadgpz.png)
Now, we can find the y-component of the final velocity of the probe
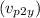 by equating it to the y-component of the final velocity of the asteroid
by equating it to the y-component of the final velocity of the asteroid
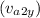 :
:
![\[v_(p2y) = v_(a2y)\]](https://img.qammunity.org/2024/formulas/physics/high-school/8jby6risc4xw1i152laqmzoxujmmi46lxw.png)
![\[300 \, \text{m/s} \cdot \sin(71^\circ) = 100 \, \text{m/s} \cdot \tan(71^\circ)\]](https://img.qammunity.org/2024/formulas/physics/high-school/yrku5fe0tppxspk0xz9fwz87u5lz0o428z.png)
Now, you can solve for the angle \(\phi\) between the x-axis and the final velocity of the probe
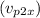 :
:
![\[\tan(\phi) = \frac{{v_(p2x)}}{{v_(p2y)}}\]](https://img.qammunity.org/2024/formulas/physics/high-school/ys1cqqoz0t535dy2i21v6ihhlgvxi2xoue.png)
![\[\phi = \tan^(-1)\left(\frac{{v_(p2x)}}{{v_(p2y)}}\right)\]](https://img.qammunity.org/2024/formulas/physics/high-school/ed5kpzgvphw7c664b6zxs9jdhko2ytzbcf.png)
Plug in the values:
![\[\phi = \tan^(-1)\left(\frac{{300 \, \text{m/s} \cdot \cos(71^\circ)}}{{300 \, \text{m/s} \cdot \sin(71^\circ)}}\right)\]](https://img.qammunity.org/2024/formulas/physics/high-school/u3zf5a60ws6frcp59y51j7npkqxs3r1ic9.png)
Let's calculate the value of
 :
:
![\[\phi = \tan^(-1)\left(\frac{{300 \, \text{m/s} \cdot \cos(71^\circ)}}{{300 \, \text{m/s} \cdot \sin(71^\circ)}}\right)\]](https://img.qammunity.org/2024/formulas/physics/high-school/u3zf5a60ws6frcp59y51j7npkqxs3r1ic9.png)
First, calculate the values of \
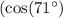 and \
and \
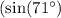 :
:
![\[\cos(71^\circ) \approx 0.2756\]](https://img.qammunity.org/2024/formulas/physics/high-school/xo08vlknxcg4n2v8220hl9vlmef1zex40x.png)
![\[\sin(71^\circ) \approx 0.9613\]](https://img.qammunity.org/2024/formulas/physics/high-school/3gm2e7nhn3ll2f3cmud3edgcpfqed7rdo4.png)
Now, substitute these values into the expression for \(\phi\):
![\[\phi \approx \tan^(-1)\left(\frac{{300 \, \text{m/s} \cdot 0.2756}}{{300 \, \text{m/s} \cdot 0.9613}}\right)\]](https://img.qammunity.org/2024/formulas/physics/high-school/wol7bgh6r792bpgkw8iz8wf85mjmddzrkl.png)
Now, calculate the value:
![\[\phi \approx \tan^(-1)(0.2864)\]](https://img.qammunity.org/2024/formulas/physics/high-school/1ppyyuag9o0jjgk9qz1q3pl3n0r25xzgeb.png)
Use a calculator to find the arctangent:
![\[\phi \approx 15.76^\circ\]](https://img.qammunity.org/2024/formulas/physics/high-school/t2lyc95x87u28dhdbtsklr0wbccmzhdz12.png)
So, the direction of the probe's final velocity is approximately
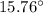 with respect to the x-axis.
with respect to the x-axis.