Question

Equation of this graph

Answer 1

The equation of the graph is: y =
`-x^2`

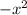
The equation of the graph appears to be a quadratic function with a vertex at (0, 0). I can't tell the exact equation from the image, but I can give you a general form and help you find the specific coefficients.

The general form of a quadratic equation with a vertex at (0, 0) is:

y = a
`x^2`

where "a" is a coefficient that determines the shape of the parabola. If "a" is positive, the parabola opens upwards, and if "a" is negative, the parabola opens downwards.

To find the specific value of "a" in this case, you can use two points on the graph. For example, you can see from the image that the graph passes through the points (-2, -4) and (2, -4).

Substituting these points into the general equation, we get:

-4 = 4a (for the point (-2, -4))

-4 = 4a (for the point (2, -4))

Solving for "a" in both equations, we get:

a = -1

Therefore, the equation of the graph is:

y =
`-x^2`

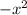
This is a downward-facing parabola with a vertex at (0, 0).